[homework-java]course02 作业

[homework-java]course02 作业

作业说明

下载 CollapsarHomeworkWeek1.java文件。拷贝到week1的包中。

打开CollapsarHomeworkWeek1.java 文件, 运行一下。

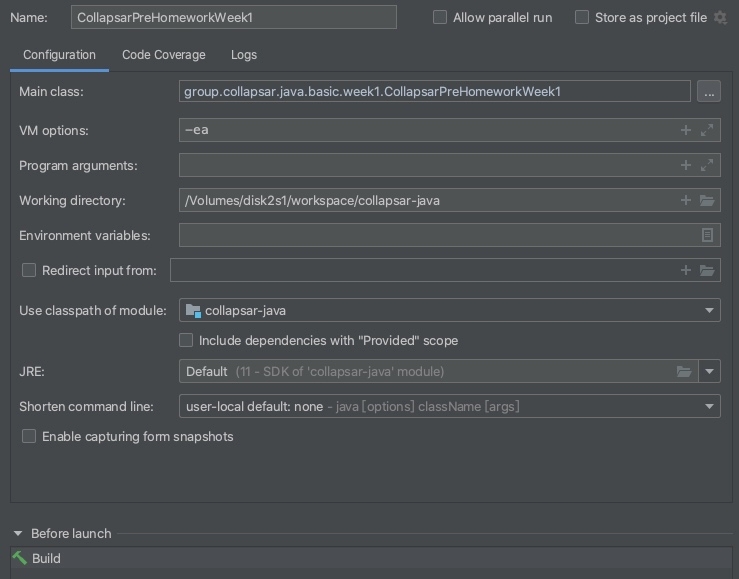
在Edit Configuration中设置对应的参数，在VM options内添加-ea参数

后面执行的时候如果看到Passed 说明用例通过，如果看到异常说明当前用例有问题，需要修改。

作业

1. boolean isEvenPositiveInt(int n)

Write the function isEvenPositiveInt(n) which, given a value n, returns True if it is even, positive, and an integer, and False otherwise.

2. int nearestOdd(double n)

Write the function nearestOdd(n) that takes a double n, and returns as an int value the nearest odd number to n. In the case of a tie, return the smaller odd value. Note that the result must be an int, so nearestOdd(13.0) is the int 13, and not the float 13.0.

3. int getTheCents(double n)

Write the function getTheCents(n) which takes a value n (which represents a payment in US dollars) and returns the number of cents in the payment. For example, if n is 2.45, the function should return 45. If n is an integer, the function should return 0, as it has 0 cents; if it isn't a number, it should return None, because a non-number payment make no cents (ha!). If the payment has partial cents (for example, 3.953), it should be rounded up to the nearest cent (in this example, 96 cents).

4. boolean isPerfectSquare(double n)

Write the function isPerfectSquare(n) that takes a possibly-non-double value, and returns True if it is a double that is a perfect square (that is, if there exists an integer m such that m**2 == n), and False otherwise.

5. int numberOfPoolBalls(int rows)

Pool balls are arranged in rows where the first row contains 1 pool ball and each row contains 1 more pool ball than the previous row. Thus, for example, 3 rows contain 6 total pool balls (1+2+3). With this in mind, write the function numberOfPoolBalls(rows) that takes a non-negative int value, the number of rows, and returns another int value, the number of pool balls in that number of full rows. For example, numberOfPoolBalls(3) returns 6. We will not limit our analysis to a "rack" of 15 balls. Rather, our pool table can contain an unlimited number of rows. For this problem and the next, you should research Triangular Numbers.

6. int numberOfPoolBallRows(int balls)

This problem is the inverse of the previous problem. Write the function numberOfPoolBallRows(balls) that takes a non-negative int number of pool balls, and returns the smallest int number of rows required for the given number of pool balls. Thus, numberOfPoolBallRows(6) returns 3. Note that if any balls must be in a row, then you count that row, and so numberOfPoolBallRows(7) returns 4 (since the 4th row must have a single ball in it).

7. Integer colorBlender(int rgb1, int rgb2, int rgb3, int n)

This problem implements a color blender, inspired by this tool. In particular, we will use it with integer RGB values (it also does hex values and RGB% values, but we will not use those modes). Note that RGB values contain 3 integers, each between 0 and 255, representing the amount of red, green, and blue respectively in the given color, where 255 is "entirely on" and 0 is "entirely off".

For example, consider this case. Here, we are combining crimson (rgb(220, 20, 60)) and mint (rgb(189, 252, 201)), using 3 midpoints, to produce this palette (using our own numbering convention for the colors, starting from 0, as the tool does not number them):

color0: rgb(220, 20, 60) color1: rgb(212, 78, 95) color2: rgb(205, 136, 131) color3: rgb(197, 194, 166) color4: rgb(189, 252, 201)

There are 5 colors in the palette because the first color is crimson, the last color is mint, and the middle 3 colors are equally spaced between them.

So we could ask: if we start with crimson and go to mint, with 3 midpoints, what is color #1? The answer then would be rgb(212, 78, 95).

One last step: we need to represent these RGB values as a single integer. To do that, we'll use the first 3 digits for red, the next 3 for green, the last 3 for blue, all in base 10 (decimal, as you are accustomed to). Hence, we'll represent crimson as the integer 220020060, and mint as the integer 189252201.

With all that in mind, write the function colorBlender(rgb1, rgb2, midpoints, n), which takes two integers representing colors encoded as just described, a non-negative integer number of midpoints, and a non-negative integer n, and returns the nth color in the palette that the tool creates between those two colors with that many midpoints. If n is out of range (too small or too large), return None.

For example, following the case above: colorBlender(220020060, 189252201, 3, 1) returns 212078095

Hints: RGB values must be ints, not floats. Also, remember to use roundHalfUp(n) instead of round(n) when calculating midpoint colors.